March 6th Update: Microsoft appears to have updated the www.browserchoice.eu website and corrected the error I describe in this post. More details on the fix can be found in The New & Improved Microsoft Shuffle. However, I think you will still find the following analysis interesting.
-Rob
Introduction
The story first hit in last week on the Slovakian tech site DSL.sk. Since I am not linguistically equipped to follow the Slovakian tech scene, I didn’t hear about the story until it was brought up in English on TechCrunch. The gist of these reports is this: DSL.sk did a test of the “ballot” screen at www.browserchoice.eu, used in Microsoft Windows 7 to prompt the user to install a browser. It was a Microsoft concession to the EU, to provide a randomized ballot screen for users to select a browser. However, the DSL.sk test suggested that the ordering of the browsers was far from random.
But this wasn’t a simple case of Internet Explorer showing up more in the first position. The non-randomness was pronounced, but more complicated. For example, Chrome was more likely to show up in one of the first 3 positions. And Internet Explorer showed up 50% of the time in the last position. This isn’t just a minor case of it being slightly random. Try this test yourself: Load www.browserchoice.eu, in Internet Explorer, and press refresh 20 times. Count how many times the Internet Explorer choice is on the far right. Can this be right?
The DLS.sk findings have lead to various theories, made on the likely mistaken theory that this is an intentional non-randomness. Does Microsoft have secret research showing that the 5th position is actually chosen more often? Is the Internet Explorer random number generator not random? There were also comments asserting that the tests proved nothing, and the results were just chance, and others saying that the results are expected to be non-random because computers can only make pseudo-random numbers, not genuinely random numbers.
Maybe there was cogent technical analysis of this issue posted someplace, but if there was, I could not find it. So I’m providing my own analysis here, a little statistics and a little algorithms 101. I’ll tell you what went wrong, and how Microsoft can fix it. In the end it is a rookie mistake in the code, but it is an interesting mistake that we can learn from, so I’ll examine it in some depth.
Are the results random?
The ordering of the browser choices is determined by JavaScript code on the BrowserChoice.eu web site. You can see the core function in the GenerateBrowserOrder function. I took that function and supporting functions, put it into my own HTML file, added some test driver code and ran it for 10,000 iterations on Internet Explorer. The results are as follows:
| Position | I.E. | Firefox | Opera | Chrome | Safari |
|---|---|---|---|---|---|
| 1 | 1304 | 2099 | 2132 | 2595 | 1870 |
| 2 | 1325 | 2161 | 2036 | 2565 | 1913 |
| 3 | 1105 | 2244 | 1374 | 3679 | 1598 |
| 4 | 1232 | 2248 | 1916 | 590 | 4014 |
| 5 | 5034 | 1248 | 2542 | 571 | 605 |
| Position | I.E. | Firefox | Opera | Chrome | Safari |
|---|---|---|---|---|---|
| 1 | 0.1304 | 0.2099 | 0.2132 | 0.2595 | 0.1870 |
| 2 | 0.1325 | 0.2161 | 0.2036 | 0.2565 | 0.1913 |
| 3 | 0.1105 | 0.2244 | 0.1374 | 0.3679 | 0.1598 |
| 4 | 0.1232 | 0.2248 | 0.1916 | 0.0590 | 0.4014 |
| 5 | 0.5034 | 0.1248 | 0.2542 | 0.0571 | 0.0605 |
This confirms the DSL.sk results. Chrome appears more often in one of the first 3 positions and I.E. is most likely to be in the 5th position.
You can also see this graphically in a 3D bar chart:
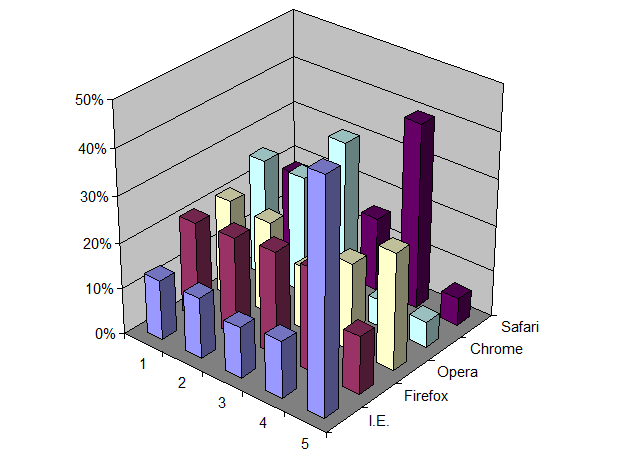
But is this a statistically significant result? I think most of us have an intuitive feeling that results are more significant if many tests are run, and if the results also vary much from an even distribution of positions. On the other hand, we also know that a finite run of even a perfectly random algorithm will not give a perfectly uniform distribution. It would be quite unusual if every cell in the above table was exactly 2,000.
This is not a question one answers with debate. To go beyond intuition you need to perform a statistical test. In this case, a good test is Pearson’s Chi-square test, which tests how well observed results match a specified distribution. In this test we assume the null-hypothesis that the observed data is taken from a uniform distribution. The test then tells us the probability that the observed results can be explained by chance. In other words, what is the probability that the difference between observation and a uniform distribution was just the luck of the draw? If that probability is very small, say less than 1%, then we can say with high confidence, say 99% confidence, that the positions are not uniformly distributed. However, if the test returns a larger number, then we cannot disprove our null-hypothesis. That doesn’t mean the null-hypothesis is true. It just means we can’t disprove it. In the end we can never prove the null hypothesis. We can only try to disprove it.
Note also that having a uniform distribution is not the same as having uniformly distributed random positions. There are ways of getting a uniform distribution that are not random, for example, by treating the order as a circular buffer and rotating through the list on each invocation. Whether or not randomization is needed is ultimately dictated by the architectural assumptions of your application. If you determine the order on a central server and then serve out that order on each innovation, then you can use non-random solutions, like the rotating circular buffer. But if the ordering is determined independently on each client, for each invocation, then you need some source of randomness on each client to achieve a uniform distribution overall. But regardless of how you attempt to achieve a uniform distribution the way to test it is the same, using the Chi-square test.
Using the open source statistical package R, I ran the chisq.test() routine on the above data. The results are:
X-squared = 13340.23, df = 16, p-value < 2.2e-16
The p-value is much, much less than 1%. So, we can say with high confidence that the results are not random.
Repeating the same test on Firefox is also non-random, but in a different way:
| Position | I.E. | Firefox | Opera | Chrome | Safari |
|---|---|---|---|---|---|
| 1 | 2494 | 2489 | 1612 | 947 | 2458 |
| 2 | 2892 | 2820 | 1909 | 1111 | 1268 |
| 3 | 2398 | 2435 | 2643 | 1891 | 633 |
| 4 | 1628 | 1638 | 2632 | 3779 | 323 |
| 5 | 588 | 618 | 1204 | 2272 | 5318 |
| Position | I.E. | Firefox | Opera | Chrome | Safari |
|---|---|---|---|---|---|
| 1 | 0.2494 | 0.2489 | 0.1612 | 0.0947 | 0.2458 |
| 2 | 0.2892 | 0.2820 | 0.1909 | 0.1111 | 0.1268 |
| 3 | 0.2398 | 0.2435 | 0.2643 | 0.1891 | 0.0633 |
| 4 | 0.1628 | 0.1638 | 0.2632 | 0.3779 | 0.0323 |
| 5 | 0.0588 | 0.0618 | 0.1204 | 0.2272 | 0.5318 |
On Firefox, Internet Explorer is more frequently in one of the first 3 positions, while Safari is most often in last position. Strange. The same code, but vastly different results.
The results here are also highly significant:
X-squared = 14831.41, df = 16, p-value < 2.2e-16
So given the above, we know two things: 1) The problem is real. 2) The problem is not related to a flaw only in Internet Explorer.
In the next section we look at the algorithm and show what the real problem is, and how to fix it.
Random shuffles
The browser choice screen requires what we call a “random shuffle”. You start with an array of values and return those same values, but in a randomized order. This computational problem has been known since the earliest days of computing. There are 4 well-known approaches: 2 good solutions, 1 acceptable (“good enough”) solution that is slower than necessary, and 1 bad approach that doesn’t really work. Microsoft appears to have picked the bad approach. But I do not believe there is some nefarious intent to this bug. It is more in the nature of a “naive” algorithm”, like the bubble sort, that inexperienced programmers inevitably will fall upon when solving a given problem. I bet if we gave this same problem to 100 freshmen computer science majors, at least one of them would make the same mistake. But with education and experience, one learns about these things. And one of the things one learns early on is to reach for Knuth.
The Art of Computer Programming, Vol. 2, section 3.4.2 “Random sampling and shuffling” describes two solutions:
- If the number of items to sort is small, then simply put all possible orderings in a table and select one ordering at random. In our case, with 5 browsers, the table would need 5! = 120 rows.
- “Algorithm P” which Knuth attributes to Moses and Oakford (1963), but is now known to have been anticipated by Fisher and Yates (1938) so it is now called the Fisher-Yates Shuffle.
Another solution, one I use when I need a random shuffle in a database or spreadsheet, is to add a new column, fill that column with random numbers and then sort by that column. This is very easy to implement in those environments. However, sorting is an O(N log N) operation where the Fisher-Yates algorithm is O(N), so you need to keep that in mind if performance is critical.
Microsoft used none of these well-known solutions in their random solution. Instead they fell for the well-known trap. What they did is sort the array, but with a custom-defined comparison function or “comparator”. JavaScript, like many other programming languages, allows a custom comparator function to be specified. In the case of JavaScript, this function takes two indexes into the value array and returns a value which is:
- <0 if the value at the first index should be sorted before the value at the second index
- 0 if the values at the first index and the second index are equal, which is to say you are indifferent as to what order they are sorted
- >0 if the value at the first index should be sorted after the value at the second index
This is a very flexible approach, and allows the programmer to handle all sorts of sorting tasks, from making case-insensitive sorts to defining locale-specific collation orders, etc..
In this case Microsoft gave the following comparison function:
function RandomSort (a,b)
{
return (0.5 - Math.random());
}
Since Math.random() should return a random number chosen uniformly between 0 and 1, the RandomSort() function will return a random value between -0.5 and 0.5. If you know anything about sorting, you can see the problem here. Sorting requires a self-consistent definition of ordering. The following assertions must be true if sorting is to make any sense at all:
- If a<b then b>a
- If a>b then b<a
- If a=b then b=a
- if a<b and b<c then a<c
- If a>b and b>c then a>c
- If a=b and b=c then a=c
All of these statements are violated by the Microsoft comparison function. Since the comparison function returns random results, a sort routine that depends on any of these logical implications would receive inconsistent information regarding the progress of the sort. Given that, the fact that the results were non-random is hardly surprising. Depending on the exact search algorithm used, it may just do a few exchanges operations and then prematurely stop. Or, it could be worse. It could lead to an infinite loop.
Fixing the Microsoft Shuffle
The simplest approach is to adopt a well-known and respected algorithm like the Fisher-Yates Shuffle, which has been known since 1938. I tested with that algorithm, using a JavaScript implementation taken from the Fisher-Yates Wikpedia page, with the following results for 10,000 iterations in Internet Explorer:
| Position | I.E. | Firefox | Opera | Chrome | Safari |
|---|---|---|---|---|---|
| 1 | 2023 | 1996 | 2007 | 1944 | 2030 |
| 2 | 1906 | 2052 | 1986 | 2036 | 2020 |
| 3 | 2023 | 1988 | 1981 | 1984 | 2024 |
| 4 | 2065 | 1985 | 1934 | 2019 | 1997 |
| 5 | 1983 | 1979 | 2092 | 2017 | 1929 |
| Position | I.E. | Firefox | Opera | Chrome | Safari |
|---|---|---|---|---|---|
| 1 | 0.2023 | 0.1996 | 0.2007 | 0.1944 | 0.2030 |
| 2 | 0.1906 | 0.2052 | 0.1986 | 0.2036 | 0.2020 |
| 3 | 0.2023 | 0.1988 | 0.1981 | 0.1984 | 0.2024 |
| 4 | 0.2065 | 0.1985 | 0.1934 | 0.2019 | 0.1997 |
| 5 | 0.1983 | 0.1979 | 0.2092 | 0.2017 | 0.1929 |
Applying Pearson’s Chi-square test we see:
X-squared = 21.814, df = 16, p-value = 0.1493
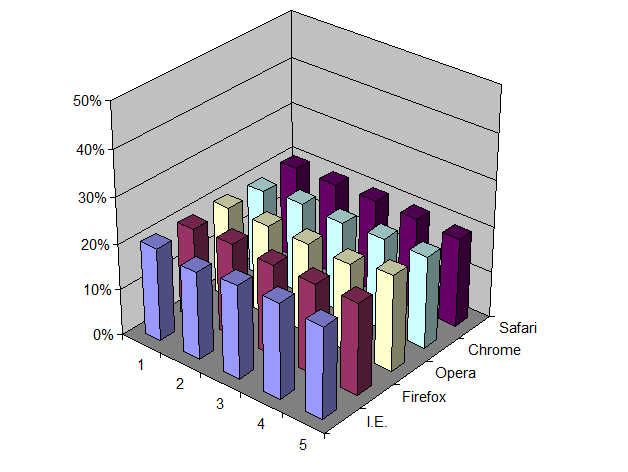
In other words, these results are not significantly different than a truly random distribution of positions. This is good. This is what we want to see.
Here it is, in graphical form, to the same scale as the “Microsoft Shuffle” chart earlier:
Summary
The lesson here is that getting randomness on a computer cannot be left to chance. You cannot just throw Math.random() at a problem and stir the pot, and expect good results. Random is not the same as being casual. Getting random results on a deterministic computer is one of the hardest things you can do with a computer and requires deliberate effort, including avoiding known traps. But it also requires testing. Where serious money is on the line, such as with online gambling sites, random number generators and shuffling algorithms are audited, tested and subject to inspection. I suspect that the stakes involved in the browser market are no less significant. Although I commend DSL.sk for finding this issue in the first place, I am astonished that the bug got as far as it did. This should have been caught far earlier, by Microsoft, before this ballot screen was ever made public. And if the EC is not already demanding a periodic audit of the aggregate browser presentation orderings, I think that would be a prudent thing to do.
If anyone is interested, you can take a look at the file I used for running the tests. You type in an iteration count and press the execute button. After a (hopefully) short delay you will get a table of results, using the Microsoft Shuffle as well as the Fisher-Yates Shuffle. With 10,000 iterations you will get results in around 5 seconds. Since all execution is in the browser, use larger numbers at your own risk. At some large value you will presumably run out of memory, time out, hang, or otherwise get an unsatisfactory experience.


